Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 검정
- p-value
- 고유벡터
- 리샘플링
- 모집단
- 신뢰구간
- 데이터분석면접
- 확률모형
- 통계
- 표본
- 선형대수
- 확률분포
- 검정력
- 통계면접
- 누적분포함수
- Transformer
- 샘플링
- 고유값
- 확률밀도함수
- 평균
- ViT
- 베타분포
- 데이터분석
- 상관계수
- 확률
- 모평균
- 확률변수
- 조건부확률
- 공분산
- Self-attention
Archives
- Today
- Total
AIMS Study Blog
R square 의 의미 본문
Q. R square 의 의미는 무엇일까요?
R square, 결정계수로 회귀 모델에서 독립변수가 종속변수를 얼만큼 설명해주는지를 가리키는 지표로 쓰인다.
설명력이라고 부르기도 한다. 결정계수가 높을수록 독립변수가 종속변수를 많이 설명한다는 뜻으로, 독립변수의 수가 증가하면 상승한다.

여기서 B 부분이 R square이다.
간단하게 생각하면 R square = 설명된분산 / 종속변수의 분산 으로 볼 수 있다.
R square의 공식
R square의 공식은 다음과 같다.

SST: Total Sum of Squares, 관측값에서 관측값의 평균을 뺀 총합, 독립변수 Y의 분산이다.
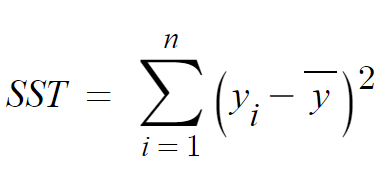
SSR: Residual Sum of Squares, 관측값에서 추정값을 뺀 잔차의 총합으로, 설명되지 않은 분산(겹치지 않는 부분, A)이다.

SSE: Explained Sum of Squares, 추정값에서 관측값의 평균을 뺀 결과의 총합으로, 설명된 분산(겹치는 부분, B)이다.

R square는 0~1의 값으로 존재하며,
1에 가까울수록 모델의 설명력이 100%라는 뜻이다.
Comments

