Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 확률모형
- 상관계수
- 리샘플링
- ViT
- p-value
- 샘플링
- 조건부확률
- 검정력
- 신뢰구간
- 확률
- 검정
- 누적분포함수
- 데이터분석면접
- 고유값
- 확률밀도함수
- 고유벡터
- 확률분포
- 선형대수
- 통계
- 평균
- Self-attention
- 통계면접
- 표본
- 공분산
- 모집단
- 확률변수
- 데이터분석
- Transformer
- 베타분포
- 모평균
Archives
- Today
- Total
AIMS Study Blog
R제곱에 대하여 본문
선형 회귀 분석을 할 때 종속변수의 분산 중에서 독립변수로 설명되는 비율이 R제곱입니다. 즉, 설명된 분산을 종속변수의 전체 분산으로 나누어준 것인데, R제곱이 높을수록 모델(독립변수)이 종속변수를 많이 설명한 것입니다. 이때 설명을 잘한다는 것, 즉 설명력이 높다는 것은 회귀 분석 시 데이터들이 회귀직선에 많이 밀집되어 있는 경우를 말합니다.
결국 R제곱이라는 것이 의미하는 것은, 회귀 직선에 데이터가 얼마나 밀접하게 분포가 되는지를 의미합니다. 일반적으로 R제곱 값(0~1)이 클수록 예측되는 값의 정밀도가 높아집니다.
그런데 R제곱은 독립변수가 많을수록 늘어나는 성질이 있어서 설명력의 정확한 척도가 되지 않을수도 있습니다. 그래서 adjusted R제곱을 사용하기도 합니다.
R제곱의 수식은 다음과 같습니다.
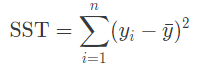


'통계' 카테고리의 다른 글
| 평균과 중앙값 (0) | 2023.02.25 |
|---|---|
| R square 의 의미 (0) | 2023.02.18 |
| A/B Test (0) | 2023.02.18 |
| A/B Test (0) | 2023.02.18 |
| R-squared 란? (0) | 2023.02.18 |
Comments

