| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- ViT
- 확률변수
- 확률분포
- 선형대수
- 데이터분석
- 확률모형
- 통계
- 표본
- 모평균
- 누적분포함수
- 베타분포
- 통계면접
- 평균
- 확률
- 검정
- 신뢰구간
- 확률밀도함수
- 공분산
- 리샘플링
- 검정력
- Transformer
- p-value
- 상관계수
- Self-attention
- 모집단
- 고유값
- 샘플링
- 조건부확률
- 데이터분석면접
- 고유벡터
- Today
- Total
AIMS Study Blog
확률 밀도 함수와 확률 질량 함수 그리고 누적 분포 함수 본문
확률 밀도 함수, 확률 질량 함수, 누적 분포함수는 무엇인가요?
확률 밀도 함수 / 확률 질량 함수
- 확률 질량 함수 (PMF : Probability Mass Function) : 이산 확률 변수 X의 분포를 나타내는 함수
- 확률 밀도 함수 (PDF : Probability Density Function) : 연속 확률 변수 X의 분포를 나타내는 함수
확률 질량 함수에서는 각 지점에 대한 확률이 함수 값과 동일하다고 볼 수 있지만, 확률 밀도 함수에서는 각 지점의 함수 값이 확률을 의미하는 것이 아니라 정해진 구간에 따른 넓이가 확률 값과 동일하다.
"왜 이산 확률 변수의 분포는 질량이라는 표현을 쓰고, 연속 확률 변수의 분포는 밀도라는 표현을 쓰는 것인가?"
물리학과 관련해서 질량과 밀도의 관계를 나타내는 대표적인 수식은 다음과 같다.


여기에서 부피는 V, 질량은 m, 밀도는 ρ(rho)로 표현을 한 수식이다. 하지만, 위의 수식의 전제는 물체의 밀도가 모든 곳에서 균일하다는 가정을 하고 있다. 물체의 밀도가 위치마다 다른 경우에는 밀도를 물체 내부의 함수로 정의해야 한다.

따라서 질량은 아래와 같은 적분 식으로 표현이 될 수 있다.

이것을 1차원으로 표현을 하게 되면 다음과 같다.

질량이 위치마다 다른 직선이 있다고 가정을 했을 때, 직선의 전체 혹은 일부분에 대한 질량을 구하기 위해서는 적분 식을 통해서 구해야 한다. 밀도에 대한 함수를 알고 있다면 0 ~ x까지의 직선의 질량을 구하기 위해서 다음의 식으로 표현이 된다.

이번에는 직선이 아닌 질량을 가지고 있는 점들이 간격을 두고 위치해 있다고 가정을 하고, 특정 위치(d)까지의 질량을 구하기 위해서는 다음의 식을 사용할 수 있다.

위의 두 식이 각각 연속 확률 분포의 확률 값과 이산 확률 분포의 확률 값을 계산하는 공식과 동일하여 연속 확률 분포의 함수에는 '밀도'라는 단어가, 이산 확률 분포의 함수에는 '질량'이라는 단어가 들어갔다고 볼 수 있을 것이다.
누적 분포 함수
누적 분포 함수 (CDF : Cumulative Distribution Function) :
해당 확률 변수의 값보다 작거나 같은 확률 변수 값들에 대한 확률을 나타내는 함수이다.
누적 분포 함수를 F라고 가정 했을 때, 누적 분포 함수 값은 다음과 같이 정의된다.
- 이산 확률 변수
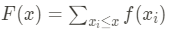
- 연속 확률 변수

Answer.
확률 질량 함수는 이산 확률 변수의 분포를 나타내는 함수이며, 확률 밀도 함수는 연속 확률 변수의 분포를 나타내는 함수이다. 확률 질량 함수는 해당 지점에서의 함수 값이 확률 값과 동일하지만, 확률 밀도 함수는 지점이 아닌 구간의 넓이와 확률이 동일하다.
누적 분포 함수는 확률 질량 함수와 확률 밀도 함수에서 특정 확률 변수의 값보다 작은 값들의 확률 값을 전부 누적한 값을 해당 확률 변수의 값으로 가지는 함수로 0에서 시작하여 마지막 확률 변수의 값에서는 1의 값을 가지게 된다.
Ref.
'통계' 카테고리의 다른 글
| 확률 모형 및 확률 변수에 대해 (0) | 2023.01.22 |
|---|---|
| 누적 분포 함수와 확률 밀도 함수 (0) | 2023.01.22 |
| 확률 밀도 함수와 누적 분포 함수 (0) | 2023.01.21 |
| 확률 변수와 확률 모형 (0) | 2023.01.21 |
| 확률 모형과 확률 변수 (0) | 2023.01.21 |


