| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Self-attention
- 고유벡터
- 조건부확률
- 베타분포
- 상관계수
- 샘플링
- 데이터분석
- 검정력
- 표본
- 확률밀도함수
- 평균
- 통계면접
- 모평균
- 모집단
- 확률
- 확률모형
- 누적분포함수
- ViT
- 확률변수
- 리샘플링
- 통계
- Transformer
- 확률분포
- 신뢰구간
- p-value
- 데이터분석면접
- 공분산
- 고유값
- 선형대수
- 검정
- Today
- Total
AIMS Study Blog
variational autoencoder 본문
본 포스팅은 아래 두 강의를 참고 하였음을 밝힙니다.
https://www.youtube.com/watch?v=GbCAwVVKaHY&list=PLQASD18hjBgyLqK3PgXZSp5FHmME7elWS&index=9
https://www.youtube.com/watch?v=rNh2CrTFpm4&t=3051s
안녕하세요. 이번 포스팅에서는 VAE에 대한 설명을 하겠습니다. VAE는 auto-encoding variational bayes라는 논문(https://arxiv.org/abs/1312.6114)에서 소개된 생성모델입니다. variational auto-encoder라는 이름 탓에 오토인코더와 같은 것이라고 생각할 수 있겠습니다만, 목적이 다른 네트워크입니다. 본 포스팅에서는 오토인코더와의 차이, 그리고 내부 구조를 중점적으로 소개하고자 합니다.
AutoEncoder
앞서 다른 발표자가 autoencoder를 다룬 내용을 기반으로 간략하게 autoencoder에 대해 짚고 넘어가겠습니다.
autoencoder는 일반적으로 manifold learning을 위한 비지도학습 모델입니다. autoencoder에는 여러 목적이 존재하지만, 고차원의 데이터에 manifold가 존재한다고 가정을 하고 저차원의 해당 manifold를 찾아내기 위해 인코더를 학습하는 것입니다. 인코더에 인풋 데이터 x(일반적으로 이미지)가 입력이 되면, 차원이 축소된 latent vector z가 나오는 형태입니다. 이를 위해서는 학습 과정에서 입력 데이터를 똑같이 복원하여 출력하는 디코더가 필요합니다. 따라서 autoencoder는 인코더와 디코더를 가진 형태를 띕니다. 아래 이미지에서 보는 것과 같이 인풋 레이어와 아웃풋 레이어는 같은 차원을 가지고 있고, 가운데 노드 수가 상대적으로 적은 레이어를 가지고 있으며, 대칭적입니다. 가운데 latent representation을 기준으로 왼쪽은 인코더, 오른쪽은 디코더가 되겠습니다.

인코더와 디코더의 복원 과정을 통해 결국 고차원 데이터에서 가정된 manifold를 찾는 것이 목적이 되겠습니다. 최종적으로 autoencoder의 목적은 인코더 학습에 있으며, 이를 위해서 디코더를 붙여서 학습을 하는 꼴이 되는 것입니다.
Variational AutoEncoder
Variational AutoEncoder(VAE)는 autoencoder와 정반대의 목적을 갖고 있습니다. VAE의 목적은 autoencoder와는 반대로 디코더 학습에 있습니다. 그리고 디코더 학습을 위해 인코더를 활용하는 것입니다. VAE의 본래 목적은 decoder로 새로운 데이터를 생성하는데에 있기 때문입니다. 여기서 둘 간의 내부적인 차이가 발생합니다. 생성모델은 학습데이터의 확률분포를 학습하여 그에 기반한 새로운 데이터를 생성해내는 것이 목표입니다. 그러기 위해서는 학습데이터의 확률분포를 알아내어 그 확률분포에서 샘플링하는 과정이 필요합니다. autoencoder의 경우 input data가 인코더를 거쳐서 나오는 것은 latent vector z뿐이고, 네트워크 자체가 deterministic하기 때문에 샘플링을 하는 부분이 존재하지 않습니다. 따라서 생성모델로서의 기능은 없다고 볼 수 있습니다. 반면, VAE의 경우 인코더에서 출력되는 것이 autoencoder와는 차이가 있습니다. 바로 z가 나오는 것이 아니고, 두 개의 파라미터가 우선 나옵니다. 그것은 가우시안 확률분포의 평균 μ와 표준편차 σ가 되겠습니다. 이 두 개의 파라미터를 통해 latent vector z의 확률분포가 정의됩니다. 그리고 해당 확률분포에서 샘플링된 z값을 decoder에 입력하여 최종적으로 output data를 출력합니다. 상술한 바에서 유추할 수 있듯, z는 가우시안 분포를 따른다고 가정합니다. 그렇게 샘플링된 z를 디코더에 넣어서 입력 데이터의 복원본을 출력합니다.
이때 의문점이 하나 생깁니다. vae는 분명 신경망으로 구성된 딥러닝 네트워크인데, 중간 latent vector z을 샘플링을 어떻게 하는지입니다. 샘플링을 일반적인 방법으로 한다고 해도 back propagation을 어떻게 하는지가 의문이 될 수도 있습니다. 이 샘플링 기법은 reparameterization trick이라는 트릭을 사용합니다. 인코더에서 출력된 평균이 0이고 표준편차가 1인 정규분포에서 ε을 샘플링하여 σ와 곱한 후 μ를 더해준 것이 z가 됩니다. 다시 말해 인코더로 정의한 정규분포에서 z를 샘플링하는 대신 reparmeterization trick을 사용하여 미분 가능한 형태로 샘플링을 해서 back propagation이 가능하게끔 만들어 주는 것입니다.

위 그림은 vae의 구조를 도식화한 것입니다.
Loss Function
VAE를 학습시키기 위한 loss function에는 두 가지 loss term이 있습니다. 수식은 후술할 예정이며, 우선은 직관적인 설명을 먼저 하겠습니다.
1. Reconstruction Error
해당 loss term은 autoencoder의 그것과 같은 것입니다. 입력 이미지를 잘 복원할 수 있도록 설계된 loss입니다. 일반적으로 네트워크의 출력값이 Gaussian Distribution을 따른다고 가정할 경우 MSE를, Bernoulli Distribution을 따른다고 가정할 경우 cross entropy를 사용하는데, VAE의 경우 보통 후자입니다. 입력 데이터와 출력 데이터의 차이를 cross entropy를 통해 계산을 하고, 이를 최소화하는 것에 목적을 두고 있습니다.
2. Regularization
복원만 하면 autoencoder입니다. VAE는 복원뿐만이 아니라, z가 normal distribution이 따른다는 가정이 존재하기 때문에, 그 가정을 최적화에 반영하기 위해서 존재하는 loss term이 regularization입니다. training data x가 주어졌을 때 encoder를 통과해서 나온 z의 확률분포가, 즉 p(z)가 normal distribution을 따를 수 있도록 최적화를 해야합니다. 그러므로 KL divergence를 사용하여 가우시안분포와 encoder의 확률 분포간의 거리를 최소화합니다.
loss에 대해 조금 더 깊게 다뤄보겠습니다.
디코더의 목적은 갖고 있는 training data의 likelihood를 최대화하는 것입니다. 즉, 갖고 있는 데이터의 확률분포를 정한다는 것이고, 그 말은 네트워크의 최종단에서 training data x가 나올 확률이 가장 커지는 확률분포를 만드는 것이 목적이라는 말입니다. 결국 VAE의 출력단은 p(x)가 가장 큰 확률분포를 갖게끔 최적화가 되어야 합니다.

위 수식은 베이즈정리로부터 파생된 수식입니다. 수식의 뜻은, x와 z가 동시에 일어날 확률을 모든 z에 대해 적분을 하면 x가 발생할 확률이라는 뜻이 되겠습니다. p(z)는 어차피 z가 정규분포를 따른다고 가정을 했고, p(x|z)는 z가 주어졌을 때 x의 확률로, 디코더라는 신경망으로 구현이 되었기 때문에 문제가 없으나, 모든 z에 대해 적분을 하는 것이 intractable합니다.
그래서 다른 접근법을 생각합니다.
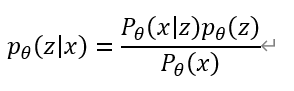
이 조건부확률 식으로부터,

위의 식이 파생됩니다. 우항의 분자는 상술했듯 알 수 있지만, 분모인 x given z의 확률을 알 수 없습니다. 여기서 인코더의 존재의 이유가 밝혀집니다. 인코더를 통해서 p(z|x)을 모델링하는 것입니다. 모델링 된 확률 분포를 q(z|x)라 씁니다.
이제 최종적으로 training data의 likelihood를 최대화 하기 위해 다음 수식을 사용합니다.
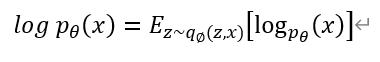
그리고 일련의 과정을 거쳐 최종적으로 아래 수식의 objective function이 나옵니다. (유도 과정은 위에 언급한 강의 영상에서 상세히 볼 수 있습니다)

reconstruction error은 x가 q를 지나서 z가 나오고, 그것이 g를 지나서 x가 나올 확률을 maximize하는 것이며, regularization은 x가 q를 통과하는 확률분포와 normal distribution으로 가정한 z의 distribution과 일치하게 만들어주는 역할을 합니다.
이상으로 VAE에 대해서 알아보았습니다.
감사합니다.
'딥러닝' 카테고리의 다른 글
| [RNN/LSTM/GRU] 순환 신경망 기반 Network 정리 (1) | 2023.07.12 |
|---|---|
| variational autoencoder 발표 영상 (0) | 2023.03.06 |
| [Transformer 모델 구조 분석] Attention Is All You Need (0) | 2023.02.13 |
| [GCN] SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS 논문 리뷰 (0) | 2023.02.02 |
| StackGAN: Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks (논문 리뷰) (0) | 2023.01.22 |



